Identificación de desliamientos en imágenes Sentinel-2

Esta página explica el trabajo desarrollado en el marco del Capstone project del Postgrado UB Datascience and Machine Learning ( http://www.ub.edu/datascience/postgraduate/ ) por los estudiantes:

Como tema para el projecto final se ha utilizado el challenge propuesto por el Institute for Advanced Research in Artificial Ingelligente accesible en el siguiente enlace: Landslide4Sense

El repositorio con el código desarrollado en el marco del proyecto puede encontrarse aquí: Repositorio

Introducción

Un deslizamiento es un tipo de corrimiento o movimiento en la masa de la tierra, provocado por la inestabilidad de un talud o ladera. Se produce cuando una gran masa de terreno se convierte en zona inestable y se desliza con respecto a una zona estable, a través de una superficie o franja de terreno de pequeño espesor. Los deslizamientos se producen cuando en la franja se alcanza la tensión tangencial máxima en todos sus puntos1.

Esquema de un deslizamiento

Esquema de un deslizamiento

Entre los años 1998 y 2017 los deslizamientos causaron más de 18.000 muertes afectando a más de 4,8 millones de personas2.

Imagen del deslizamiento ocurrido en Armero, Colombia, en 1985 Imagen del deslizamiento ocurrido en Armero, Colombia, en 1985

La identificación de deslizamientos pasados es vital para la evaluación del riesgo de ocurrencia futura de este tipo de eventos catastróficos. En los últimos años, diversos algorítmos basados en técnicas de Machine Learning aplicadas a imágenes de satélite3.

Identificación de un deslizamiento en una imagen de satélite mediante técnicas de *Machine Learning* Identificación de un deslizamiento en una imagen de satélite mediante técnicas de Machine Learning

El juego de datos de entrenamiento

El juego de datos con el que se ha realizado el presente trabajo está compuesto por 7598 ficheros *.h5 repartidos en dos carpetas, “img” y “mask”.

Carpetas

En la carpeta “img”, cada fichero *.h5 incluye 12 bandas de una imagen de los satélites Sentinel-2 más dos bandas adicionales: un modelo digital del terreno y un modelo de pendientes:

Cada banda presenta 128*128 píxeles, con una resolución de 10 m por pixel.

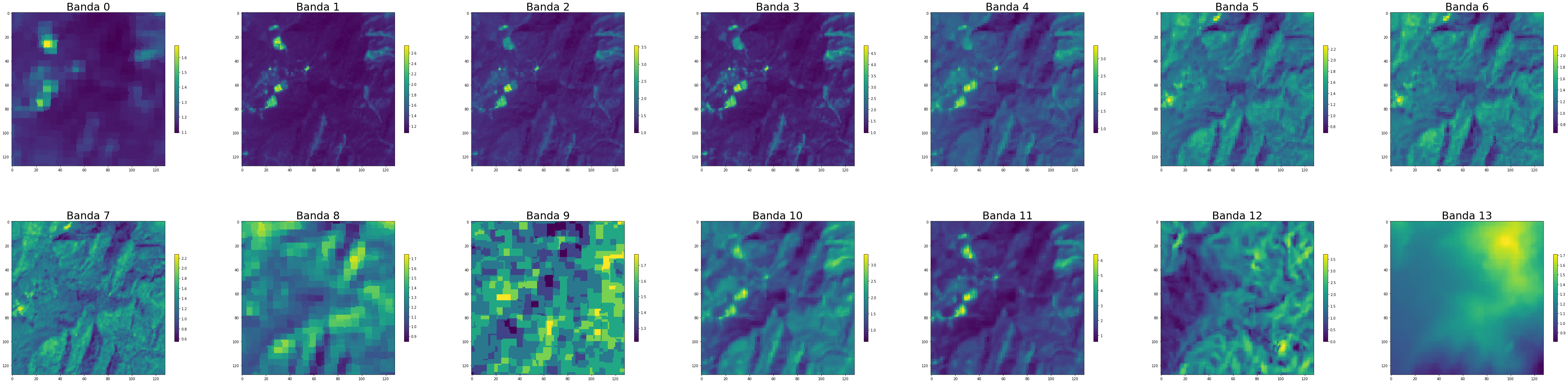Bandas en cada fichero h5 Las 14 bandas en el fichero imagen_1.h5

Por cada fichero en la carpeta “img”, con la misma numeración en el fichero, tamaño de malla (128*128), resolución (10 m) en la carpeta mask se encuentra el fichero con las etiquetas, identificando las áreas con/sin deslizamiento.

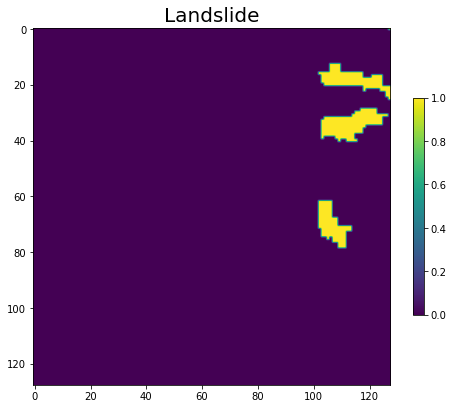
Deslizamientos etiquetados

Deslizamientos etiquetados en la imagen mask_1.h5 (mismo área que la imagen anterior, image_1.h5)

Las imágenes etiquetadas (“mask”) siguen la siguiente clasificación:

En la siguiente imagen muestra un primer análisis de la distribución de los valores para las diferentes bandas y en las zonas etiquetas con/sin deslizamiento Ver aquí en análisis completo.

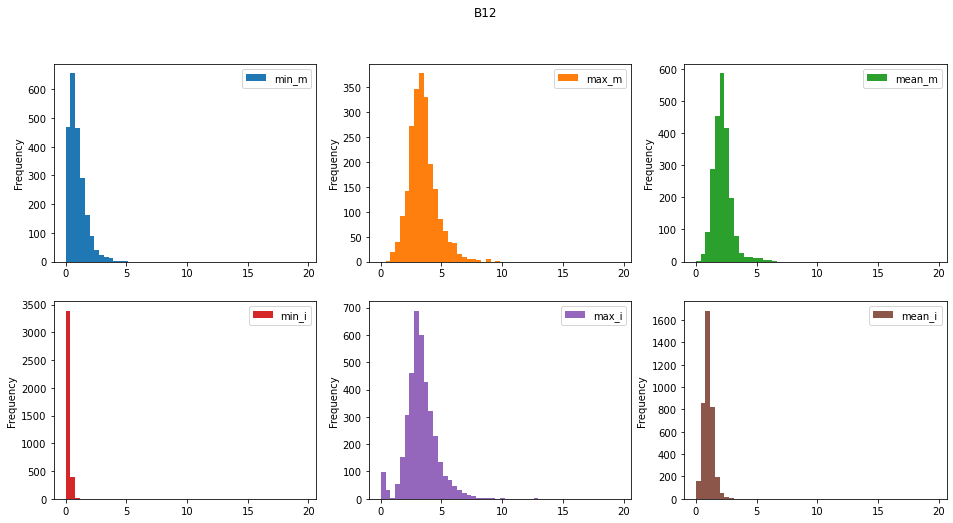
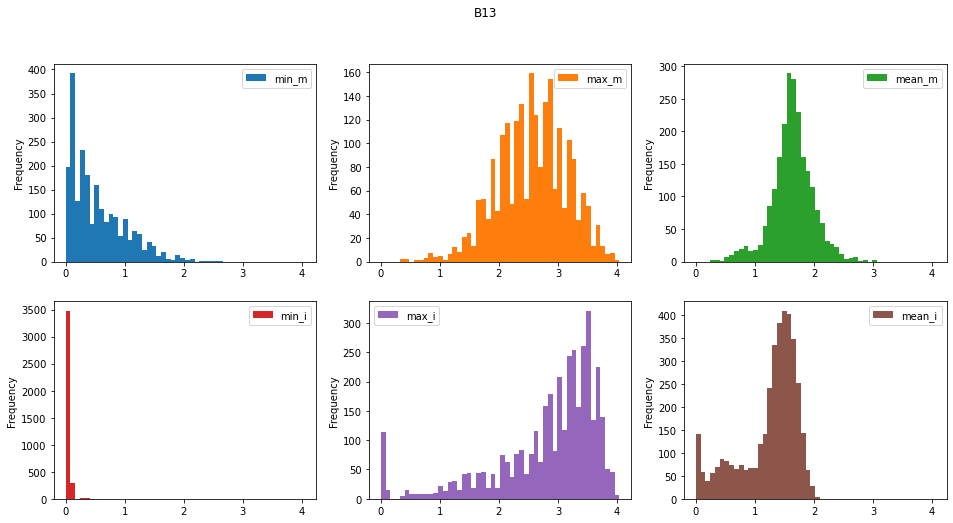
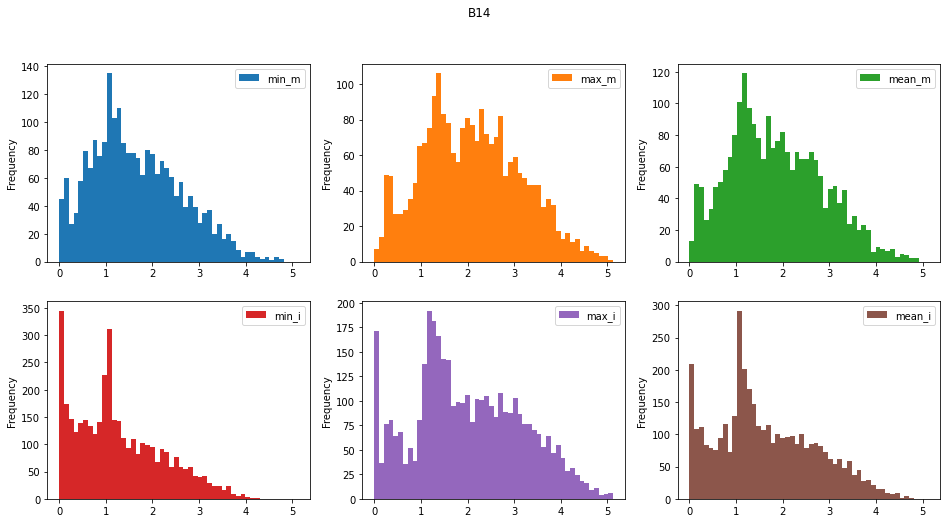
Banda 12 Banda 13 Banda 14

Para las tres bandas mostradas en la figura (Bandas 12, 13 y 13) se han generado los siguientes histogramas:

- min_m . El valor mínimo de la banda en las áreas con deslizamiento
- max_m . El valor máximo de la banda en las áreas con deslizamiento
- mean_m . El valor medio de la banda en las áreas con deslizamiento
- min_i . El valor mínimo de la banda en las áreas sin deslizamiento
- max_i . El valor máximo de la banda en las áreas sin delizamiento
- mean_i . El valor medio de la banda en las áreas con deslizamiento

Uno de los elementos que cabe mencionar del gráfico anterior es el caracter “serrado” de los histogramas de pendientes y elevaciones (DEM), bandas 13 y 14. Esto indica una concentración de celdas en torno a unos valores determinados. Aparentemente el modelo de pendientes se ha elaborado a partir del modelo digital de elevaciones (DEM). Esto podría indicar que el DEM se ha interpolado a partir de curvas de nivel (los picos indicarían los valores de las curvas de nivel que son equidistantes en un mapa 2D).

Este hecho es relevante porque nos obligará más adelante a considerar el tratamiento de estas dos bandas (pendiente y modelo digital de elevaciones).

Preprocesado de los datos

Antes de comenzar a definir los modelos, vamos a explorar varias alternativas para el preprocesado de los datos. Utilizaremos dos aproximaciones:

Creación de nuevas bandas

La revisión de la literatura científica[6^] nos indica que existen varios indicadores, generados a partir de las bandas multiespectrales estándar, que pueden ser utilizados con éxito en la identificación de deslizamientos. Nos vamos a centar en dos de estos indicadores:

Generación de nuevos indicadores a partir del DEM suavizado

Tanto el DEM como la banda de pendientes son, a priori, conjuntos de datos que pueden resultar de interés en la identificación de deslizamientos, debido a las formas características como los escarpes en cabecera o las áreas de acumulación suvazada al pie deslizamiento que podrían verse reflejadas en estas capas. Sin embargo, en las imágenes de entrenamiento (ver las imágenes de los histogramas de las bandas 13 y 14 más arriba) el histograma del modelo digital de elevaciones (DEM o MDE) y de la bande de pendientes nos muestra una agrupación de valores en determinados intervalos (¿quizás las curvas de nivel a partir de las cuales se generaron estos datos?).

Para intentar mejorar estos conjuntos de datos, se ha optado por aplicar un filtro de 5x5 para suavizar tanto el modelo digital de elevaciones como la capa de pendientes.

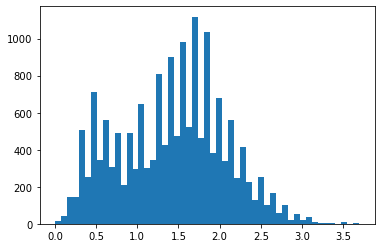
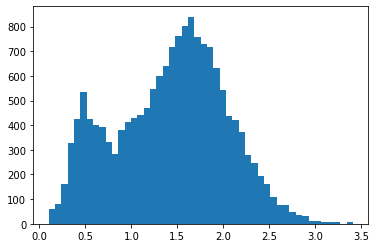
Pendiente sin suavizar Pendiente suavizada

Histograma de frecuencias para los valores de las capas/bandas de pendientes sin suavizar - izquierda - y suavizada - derecha - para la imagen imagen_1.h5

En el siguiente Notebook se evaluan varios mecanismos para el suavizado de los datos: DEM and slope denoising.ipynb

Una vez suavizado el modelo digital del terreno, es posible obtener nuevos conjuntos de datos derivados utilizando la librería RichDem8 . Los tres nuevos dataset que obtendremos a partir del DEM son9 :

Finalmente, a partir de la información original es posible obtener, para cada imagen, un nuevo conjunto de datasets.

Preprocesado de datos

El siguiente fragmento de código permite obtener estos nuevos datos para cada imagen, y es utilizando en este Notebook: UNET Model

for i, (img, mask) in enumerate(zip(all_train, all_mask)):

    with h5py.File(img) as hdf:
        ls = list(hdf.keys())
        data = np.array(hdf.get('img'))

        # assign 0 for the nan value
        data[np.isnan(data)] = 0.000001
        
        #slope and dem
        dem= data[:, :, 13]
        slope= data[:, :, 12]
        k = 5 #smoothing factor for reducing the noise
        dem_suavizado = cv.blur(dem,(k,k)) #reducción de ruido dem
        slope_suavizado = cv.blur(slope,(k,k)) #reducción de ruido slope
        
        #curvature
        dem_richdem = rd.rdarray(dem_suavizado, no_data=-9999) #convert to rdarray
        dem_curvature = rd.TerrainAttribute(dem_richdem, attrib="curvature") #calculate curvature
        dem_planform_curvature = rd.TerrainAttribute(dem_richdem, attrib="planform_curvature") #calculate planform_curvature
        dem_profile_curvature = rd.TerrainAttribute(dem_richdem, attrib="profile_curvature") #calculate profile curvature
    
        #BSI calculation
        BSI= ((data[:,:,10] + data[:,:,3]) - (data[:,:,7] + data[:,:,1]) / (data[:,:,10] + data[:,:,3]) + (data[:,:,7] + data[:,:,1]))

        # ndvi calculation
        data_red = data[:, :, 3]
        data_nir = data[:, :, 7]
        NDVI = np.divide(data_nir - data_red,np.add(data_nir, data_red))

Análisis de datos

Para el análisis hemos seguido 2 metodologías distantas:

Bandas utilizadas

En los modelos que se detallan a continuación se han utilizado 7 bandas:

Primer análisis: Modelo logístico y Modelo de clasificación Random Forest

Extracción de valores de ráster por puntos

Para implementar el modelo logístico y de Bosques Aleatorios, hemos extraído los valores de las bandas de los rásters en 100 puntos distintos (por fichero). 50 en zonas de landslide y 50 en zonas sin landslide. De esta manera hemos obtenido una base de datos con las variables respuesta (1, presencia de deslizamientos; 0, absencia de deslizamientos) y sus pertinentes valores de las bandas en 100 localidades distintas por fichero. El código para la extracción de los valores ráster por puntos se puede encontrar en el siguiente notebook Raster sampling.ipynb. La base de datos resultante se puede descargar con el siguiente enlace data_extraction.zip.

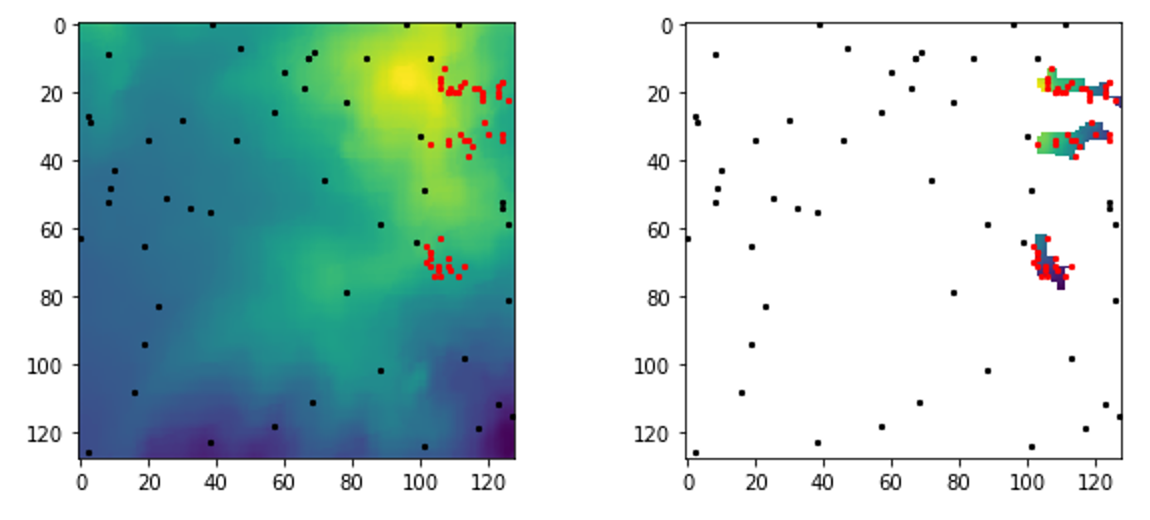
ejemplo de la extracción de puntos

Ejemplo de la disposición de las localidades para el muestreo del ráster para un fichero (en rojo zonas de landslide y en negro zonas sin landslide)

Los modelos

Los modelos están implementados en R.

Antes de crear los modelos, es buena idea hechar un vistazo a los datos: ¿Cuantas variables hay en la base de datos?, ¿Con qué tipo de datos estamos trabajando?, ¿Están normalizados?, ¿Hay NAs? También es imprescindible analizar la multicolinealidad entre las variables independientes. Si algunas variables están correlacionadas, los estimadores obtenidos y la precisión de éstos se verán afectados. Numerosos métodos han sido desarrollados para detectar multicolinealidad, por ejemplo el Factor de Inflación de la Varianza (VIF). Este índice mide hasta qué punto la varianza de un coeficiente de regresión estimado se incrementa a causa de la colinearidad. Generalmente se considera que existe un problema grave cuando el VIF excede 10. En nuestros modelos, las variables independientes no están correlacionadas.

Por último, hemos dividido el dataset en training y test para poder hacer la validación del modelo. En nuestro caso hemos usado una partición de 0.75 para training y 0.25 para test.

El primer modelo que hemos creado es un modelo de regresión logística:

m1 <- glm(pa ~dem+slope+curvature+planform_curvature+profile_curvature+NDVI+BSI , data = traindata, family = binomial(link = "logit"))

La función summary() nos regresa el sumario del modelo. Dado que en los modelos de regressión logística la relación entre p(Y) y X no es lineal, los coeficientes de regressión no se corresponden con el cambio en la probabilidad de Y asociada con el incremento de una unidad de X. De todas formas, podemos determinar si la relación entre los predictores y la ocurrencia de deslizamientos es positiva o negativa. Por ejemplo, la altitud y el pendiente tienen un efecto positivo a la ocurrencia de deslizamientos.

Coefficients:
                   Estimate Std. Error z value Pr(>|z|)    
(Intercept)        -0.21253    0.09322  -2.280   0.0226 *  
dem                 0.10808    0.02229   4.848 1.25e-06 ***
slope               0.15080    0.03578   4.215 2.50e-05 ***
curvature           0.06625    0.13186   0.502   0.6154    
planform_curvature -0.06032    0.08392  -0.719   0.4723    
profile_curvature   0.12227    0.10544   1.160   0.2462    
NDVI                0.01877    0.02270   0.827   0.4084    
BSI                 0.05302    0.03204   1.655   0.0980 .  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

El siguiente paso es hacer predicciones y validar los resultados del modelo. Para ello, hemos calculado las siguientes métricas de evaluación:

Los resultados del modelo logístico no son nada informativos ya que todas las métricas de evaluación están alrededor del 0.5.

[1] "accuracy: 0.504550395016466"
[1] "precision: 0.503479155321595"
[1] "recall: 0.540833902050632"
[1] "f1 score: 0.521488444966706"

El segundo modelo hemos implementado es un modelo de clasificación Random Forest (Bosques Aleatorios). Un Random Forest es un conjunto (ensemble) de árboles de decisión combinados con bagging (ningún árbol ve todos los datos de entrenamiento).

m2= randomForest(pa~dem+slope+curvature+planform_curvature+profile_curvature+NDVI+BSI, data=traindata,ntree=500, importance=TRUE)

Este modelo produce mejores resultados que el modelo de regresión logístico, pero sigue siendo bastante malo.

[1] "accuracy: 0.557062440179745"
[1] "precision: 0.554119446785926"
[1] "recall: 0.576809333463326"
[1] "f1 score: 0.565236775898857"

Segundo análisis: Modelo Secuencial y Modelo U-Net

Se han implementado también dos modelos utilizando técnicas de deep learning. En primer lugar se ha creado un modelo secuencial sencillo y a continuación una red convolucional de tipo U-Net. Ambos modelos se han implementado en el siguiente Notebook: UNET Model

Preprocesado de los datos

Los datos han sido preprocesados para obtener las bandas indicadas anteriormente. Se han suavizado las bandas correspondientes al MDE y a las pendientes. A partir de esta información (en concreto del DEM) se han generado las tres bandas de curvatura del terreno. Además, se han obtenido los índices NDVI y BSI. A continuación, los valores nan generados durante cálculo de los índices NDVI y BSI han sido sustituidos por 0.000001 y se han normalizado las bandas. Todos los datos de las imágenes se han integrado en un array de 4 dimensiones: el índice de la imagen, la fila y columna (128x128) y la banda, siendo las dimensiones finales (3799, 128, 128, 8).

El modelo secuencial

En primer lugar, se ha implementado un modelo secuencial con tres capas.

model_sequential.add(Dense(20, input_shape=(128, 128, 7), activation='relu')) 
model_sequential.add(Dense(10, activation='relu'))
model_sequential.add(Dense(1, activation='sigmoid'))

Se ha utilizado una función de pérdida de tipo Binary Loss Entropy, atendiendo al caracter binario del resultado esperado. Una vez ejecutado, el modelo ofrece un valor de F1 de 0.5442. En la siguiente imagen se presentan las curvas de aprendizaje de los diferentes parámetros considerados.

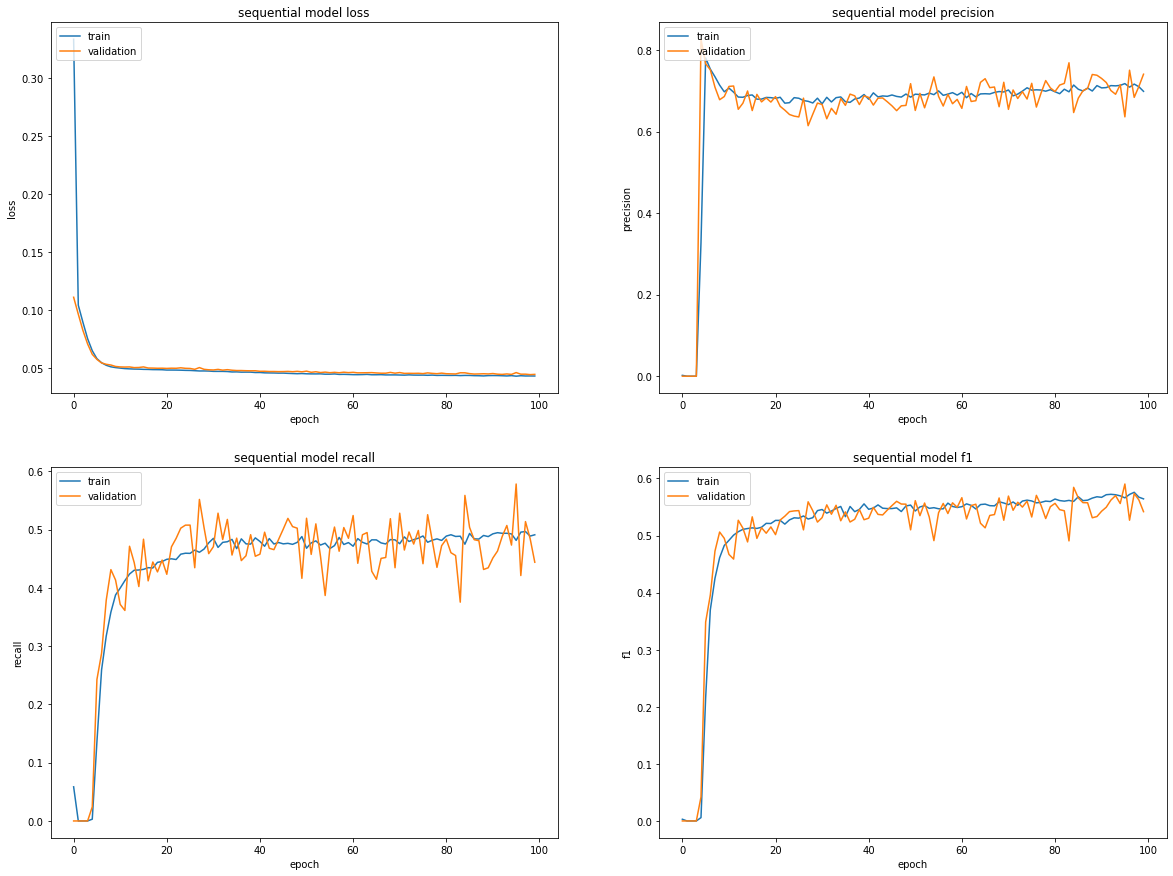Curvas de aprendizaje modelo secuencial Curvas de aprendizaje del modelo secuencial

El model U-Net

Finalmente se ha implementado un modelo de red convolucional tipo U-Net. Las características del modelo pueden verse en el Notebook UNET Model .Se ha utlizado la misma función de pérdida que en el caso anterior. Se programa el modelo para ejecutar 100 epocs. Como resultado final se obtiene un valor de F1 de 0.700610. Las curvas de aprendizaje de los parámetros se muestran a continuación.

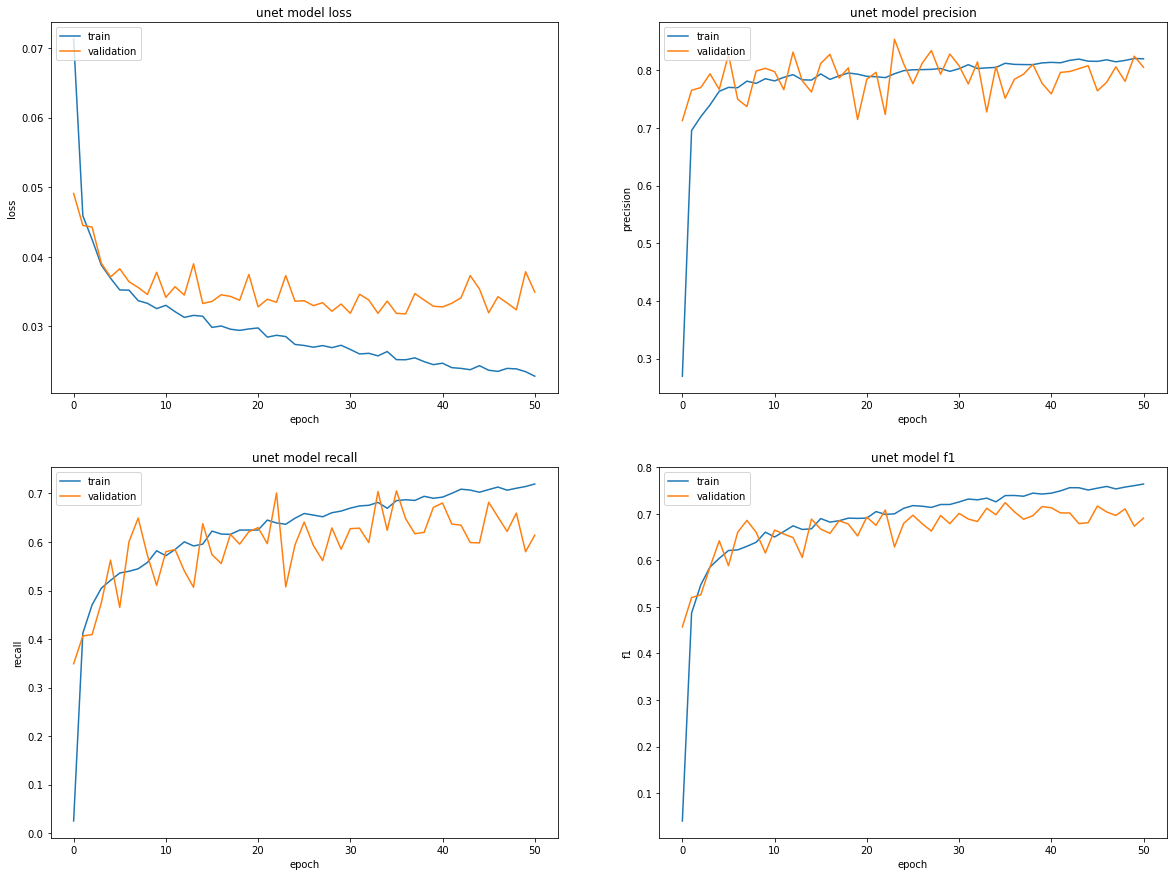Curvas de aprendizaje modelo secuencial Curvas de aprendizaje del modelo U-Net

Conclusiones

Como principal conclusión podemos indicar que el modelo de red convolucional tipo U-Net implementado permite obtener unos resultados sustancialmente mejores que los otros algoritmos empleados. La siguiente imagen muestra la diferencia entre la predición y las zonas etiquetadas inicialmente como deslizamiento.

Resultado final

En su contra, es muy exigente en el uso de recursos de computación lo que limita las posibilidades de optimización de los parámetros utilizados.

https://medium.com/sentinel-hub/landslide-detection-for-rapid-mapping-using-sentinel-2-2a84c2766a0 https://www.ggs-solutions.eu/wp-content/uploads/Landslide-Detection-in-Central-America-using-the-Differential-Bare-Soil-Index.pdf

  1. Modificado de https://es.wikipedia.org/wiki/Deslizamiento_de_tierra ↩

  2. Fuente: https://www.who.int/health-topics/landslides#tab=tab_1 ↩

  3. Ver, por ejemplo, https://link.springer.com/article/10.1007/s11069-022-05423-7 ↩

  4. Más detalles sobre las diferentes bandas en: https://www.satimagingcorp.com/satellite-sensors/other-satellite-sensors/sentinel-2a/ ↩

  5. Más información sobre los datos del proyecto Alos Palsar en https://earth.esa.int/eogateway/catalog/alos-palsar-products ↩

  6. Ver, por ejemplo, https://es.wikipedia.org/wiki/%C3%8Dndice_de_vegetaci%C3%B3n_de_diferencia_normalizada ↩

  7. Más información en https://custom-scripts.sentinel-hub.com/custom-scripts/sentinel-2/barren_soil/ ↩

  8. Ver https://richdem.readthedocs.io/en/latest/ ↩

  9. Para una explicación detallada de estos parámetros: https://richdem.readthedocs.io/en/latest/terrain_attributes.html?highlight=curvature#curvature ↩

  10. Como referencia, los equipos ganadores en el challenge en el que se basa este trabajo obtuvieron unos valores de F1 entre 0.7454 y 0.7350. El equipo que recibió el premio a la solución más innovadora obtuvo un F1 score de 0.7129. ↩